Introduction to RSA Algorithm for Cybersecurity

The RSA Algorithm is a type of public key, and its main concept can be explained using a lock and key analogy. By distributing open locks to the messengers, they are able to place their message and lock it up with a publicly distributed key and return it to the owner.

Upon receiving the package, the owner can then use their own private key to unlock the message. Thus, effective security only requires keeping the private key private; the public key can be openly distributed without compromising security.

However, in the online world, keys are generated using numbers. How can numbers possibly be secure?

The generation of keys depends on cryptographic algorithms based on mathematical problems to produce one-way functions. RSA encryption works under the premise that the algorithm is easy to compute in one direction, but almost impossible to reverse.

For instance, What is 907*773? The answer is 701111. Since such a question requires basic math, the problem is considered an easy one. However, if the question was reversed in such a way:

What are the prime factors of 701111? This question would require much trial and error in order to get the answer. (701111/11??, 701111/13?….so on). As for the computer, the time taken to find the prime factors drastically increases with the size of the number.

Since the relationship between these numbers is simple to compute in one direction, but incredibly hard in reverse, the equation is known as a trapdoor function. Be aware that while the above example is hard for people to figure out, computers can do the operation in a trivial amount of time.

Because of this, RSA uses much larger numbers. The size of the primes in a real RSA implementation varies, but in 2048-bit RSA, they would come together to make keys that are 617 digits long. To help you visualize it, a key would be a number of this size:

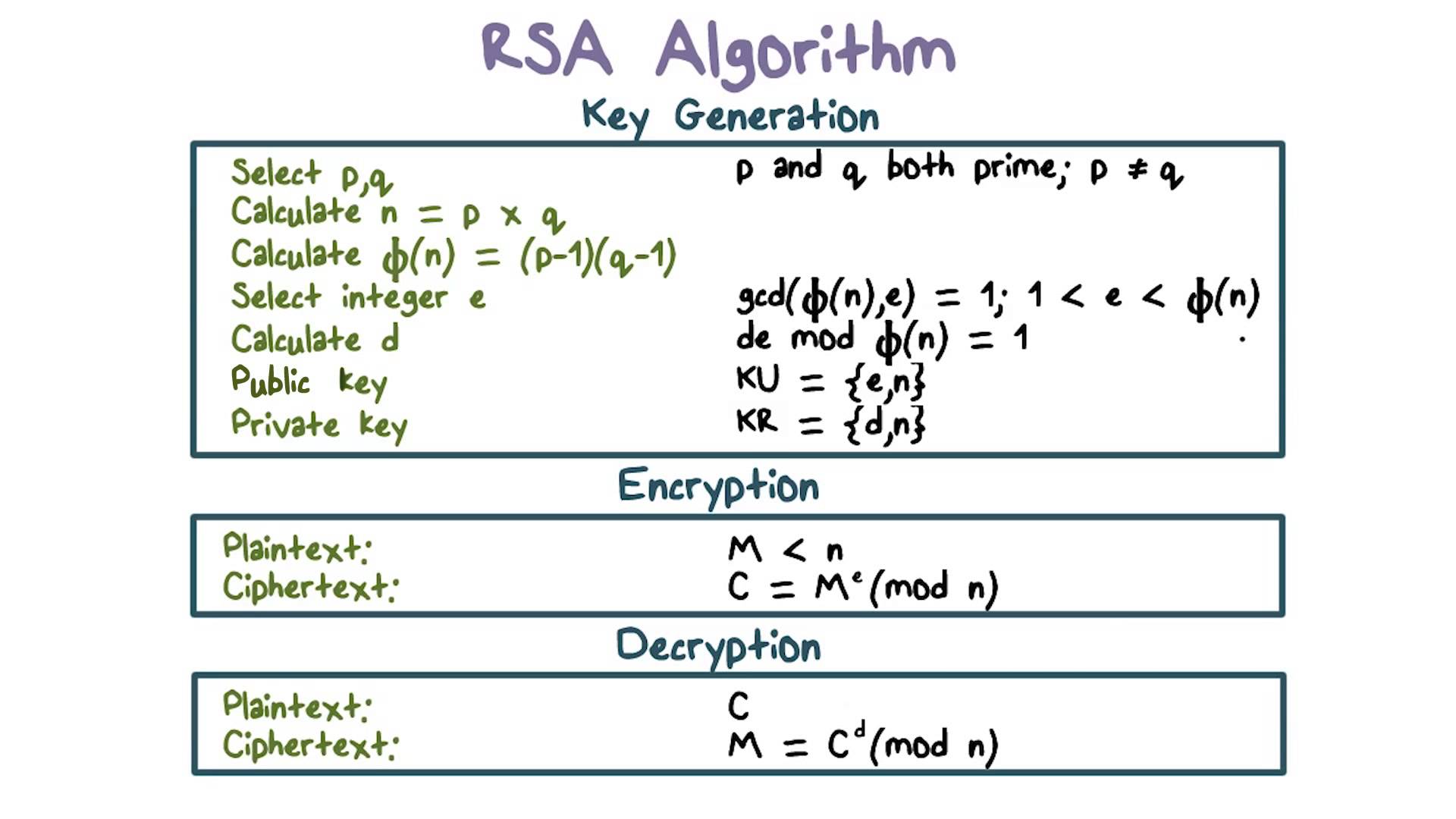
Hence, here’s the full method of RSA:

This app is designed to allow users to learn about the process of encryption, through a mini “game”. Currently, the algorithm used is the RSA Algorithm. Website: cwcr9029.pythonanywhere.com

Help Guide

Get a friend to enter a password, or enter a pin password. Try to keep it only at 6 numbers, as this was done to speed up the encryption process Using the above equation, where the Encrypted Message (C) public key(n), and the private key (d), compute the value of m (which is the encrypted message. You can either use the online calculator provided or your own calculator. If the message is correct (it should be the pin you or your friend entered), you will be redirected to the success page. If not, try again.